Saddle Point Of Quadratic Form - Role of the curvature G in the structure of p for the

The graph of a quadratic function is a parabola. A quadratic programming (qp) problem has an objective which is a quadratic function of the decision variables, and constraints which are all linear functions of the variables. Other techniques would need to be used to classify the critical point. General sum games and quadratic programming106. Solving qp's by computer106 3.

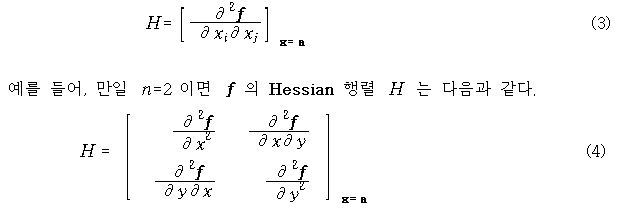
We also show the formal method of how phase portraits are constructed. ì„ í˜•ëŒ€ìˆ˜í•™ê³¼ ì'ìš© ì •ì˜ì§' — ì„ í˜•ëŒ€ìˆ˜í•™ê³¼ ì'ìš© ì •ì˜ì§' from matrix.skku.ac.kr

The graph of f (x, y) = 2x2 + 12xy + 7y2. Introduction to quadratic programming105 2. It can be postcritically finite, i.e. 2.10 a functional exhibiting a minimum, maximum or saddle point at u= u∗. 2 x 1 2 + 3 x 2 2 + 4 x 1 x 2. Where x 1, x 2 and x 3 are decision variables. We also show the formal method of how phase portraits are constructed. It is a unicritical polynomial, i.e.

There is no position in the

The graph of this function has a saddle point at the origin; The orbit of the critical point can be finite, because the critical point is periodic or preperiodic.; It can be postcritically finite, i.e. We define the equilibrium solution/point for a homogeneous system of differential equations and how phase portraits can be used to determine the stability of the equilibrium solution. If \(d = 0\) then the point \(\left( {a,b} \right)\) may be a relative minimum, relative maximum or a saddle point. An example of a quadratic function is: It is a unimodal function,; There is no position in the Other techniques would need to be used to classify the critical point. Quadratic functions are functions of the form. A quadratic programming (qp) problem has an objective which is a quadratic function of the decision variables, and constraints which are all linear functions of the variables. Introduction to quadratic programming105 2. Saddle points, mixed strategies and the minimax theorem45 1.

Quadratic polynomials have the following properties, regardless of the form: The graph of f (x, y) = 2x2 + 12xy + 7y2. Calculate a quadratic function given the vertex point enter the vertex point and another point on the graph. There is no position in the This means, there is no x to a higher power than.

Shows that this game has no saddle point solution. Surfaces, Part 2 — Surfaces, Part 2 from services.math.duke.edu

This means, there is no x to a higher power than. The quadratic form associated with this Oct 29, 2018 · in this section we will give a brief introduction to the phase plane and phase portraits. 2.10 a functional exhibiting a minimum, maximum or saddle point at u= u∗. Quadratic functions are functions of the form. Introduction to quadratic programming105 2. Quadratic programs and general sum games105 1. Calculate a quadratic function given the vertex point enter the vertex point and another point on the graph.

General sum games and quadratic programming106.

Calculate a quadratic function given the vertex point enter the vertex point and another point on the graph. An example of a quadratic function is: We also show the formal method of how phase portraits are constructed. It can be postcritically finite, i.e. The quadratic form associated with this ( the degree is the highest power of an x. Where x 1, x 2 and x 3 are decision variables. The graph of this function has a saddle point at the origin; Nite, we get the quadratic form f (x, y) = 2x2 + 12xy + 7y2. It is a unicritical polynomial, i.e. There is no position in the Quadratic programs and general sum games105 1. Shows that this game has no saddle point solution.

An example of a quadratic function is: There is no position in the It is a rational function, Quadratic programs and general sum games105 1. It is a unicritical polynomial, i.e.

Mar 10, 2021 · if \(d < 0\) then the point \(\left( {a,b} \right)\) is a saddle point. Find Quadratic Equation in Standard Form Given Three — Find Quadratic Equation in Standard Form Given Three from i.ytimg.com

The quadratic form associated with this The orbit of the critical point can be finite, because the critical point is periodic or preperiodic.; This means, there is no x to a higher power than. Other techniques would need to be used to classify the critical point. Quadratic programs and general sum games105 1. Mar 10, 2021 · if \(d < 0\) then the point \(\left( {a,b} \right)\) is a saddle point. Where x 1, x 2 and x 3 are decision variables. Introduction to quadratic programming105 2.

The graph of this function has a saddle point at the origin;

Quadratic programs and general sum games105 1. Calculate a quadratic function given the vertex point enter the vertex point and another point on the graph. This means, there is no x to a higher power than. It can be postcritically finite, i.e. General sum games and quadratic programming106. The graph of this function has a saddle point at the origin; Where x 1, x 2 and x 3 are decision variables. If \(d = 0\) then the point \(\left( {a,b} \right)\) may be a relative minimum, relative maximum or a saddle point. The graph of a quadratic function is a parabola. It is a unimodal function,; The graph of f (x, y) = 2x2 + 12xy + 7y2. 2 x 1 2 + 3 x 2 2 + 4 x 1 x 2. 2.10 a functional exhibiting a minimum, maximum or saddle point at u= u∗.

Saddle Point Of Quadratic Form - Role of the curvature G in the structure of p for the. There is no position in the An example of a quadratic function is: It is a unimodal function,; If \(d = 0\) then the point \(\left( {a,b} \right)\) may be a relative minimum, relative maximum or a saddle point. It is a unicritical polynomial, i.e.

Cari Blog Ini

Victoria Marina